Octagon
Formulas
and
The
Square Root of Two, Minus One.
Reekie's,
Earlsferry
House inspired, Theorem: the Octagon Laid to Rest, without Trig.
During my
teenage years at Waid Academy because of my admiration for
Earlsferry House with its polygon turret I became
interested in the parameters of the regular octagon; an
eight sided polygon in which all the sides are of equal
length and all the angles are of equal degree. My interested
peaked because I could not find a math book that told me
what I wanted to know relating to the subject. All referred
to the use of trigonometric functions and trigonometric
tables in which one had to be well versed and knowledgeable
to use.
Concurrent with this interest the
subject of unity (one) was a fascination of mine. By using 1 as being the length of the sides of a right angled
isosceles triangle, the length of the hypotenuse of such a
triangle is the square root of 2 which is the irrational
number 1.4142.
My ah-ha moment came when I
subtracted 1 from the square root of 2 and discovered that
the remaining number provided the formula for the multiplier
of the Width in order to find the length of the Side of a
regular octagon. (It was at a later moment that I
concluded that the square root of 2 is the multiplier of
what I called
the B dimension to find the length of the Side)
The Number 0.4142
With this number so perceived I
made up the following formulas.
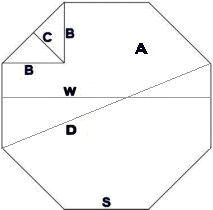
With the width of an octagon being the dimension between the parallel sides,
|
Let W be the width of the octagon
W
is also the diameter of the inscribed circle
S be
the length of the side
A be the
area
P be the
perimeter
B be the dimension at right angles to the
sides
C
be the dimension at right angles from a side to the point of
intersection at right angles from
the adjacent two sides
D
be the diagonal dimension
D is also the
diameter of the circumscribed circle
-P-
|
|
Then by
Reekie's Theorem
I deduced that:
S =
0.4142 W W = 2.4142 S
S
= 1.4142 B
B = 0.7071 S
S = 0.3826 D D
= 2.6135 S
W = 3.4142 B B
= 0.2929 W
W = 4.8284
C
C = 0.2071 W
W = 0.3018
P
P = 3.3137 W
W = 0.9239
D
D = 1.0824 W
W = The sq. rt. of (1.2071
A) A = 0.8284 W2
-----------------------------------------------------------------
Also
W = S + 2B
S = W - 2B
A = W2 - 2B2
-----------------------------------------------------------------
|
 |
|
All of these
formulas include the square root of 2.
|
0.4142 |
is the square root of 2 then - 1 |
|
1.4142 |
is
the square root of 2 |
|
2.4142 |
is the square root of 2 then + 1 |
|
3.4142 |
is
the square root of 2 then + 2 |
|
0.8284 |
is 2 times (the square root of 2
then - 1) |
|
4.8284 |
is (2 times the square root of
2) then + 2 |
|
0.2071 |
is (the
square root of 2 then - 1) then
divided by 2 |
|
1.2071 |
is (the square root of 2
then - 1) then divided by 2 then + 1 |
|
0.2929 |
is 1 - ( the square root of 2
then divided
by 2) |
|
0.7071 |
is the square root of 2
then divided by 2 |
|
0.3018 |
is the square root of 2
then + 1 then divided by 8 |
|
1.0824 |
is
the square root of [ (the square root
of 2 then - 1)2
then + 1 ] |
|
3.3137 |
is 8 times (the square root of 2
then -
1) |
|
0.3826 |
is
? |
|
0.9239 |
is
?
(I'm looking for help on these three
?'s) |
|
2.6135 |
is
? |
Pertaining
to my three numbers 0.3826, 0.9239 and 2.6135 I
haven't come up with rationale as
to their relationship to the Square Root of 2,
but I know there is. There must be one person
somewhere who will.
Bingo. Eureka.
June
1st 2009. An interested viewer took it upon
himself to figure out these three questions for
which I have not come up with rationale as to
their relationship to the square root of 2.
______________________________________________________________________
He writes
:
2.6135 is 0.9239 x 2 x the square root of 2
0.3826
is the square root of [ 1 divided by ( 2 x the
square root of 2 ) then + 4 ]
0.9239
is the square root of [ 1 divided by ( negative
2 x the square root of 2 ) then + 4 ]
_______________________________________________________________________
For an octagon with a
Width of 12 feet,
The Side length is
4.970 feet
The Area is 119.290
square feet
The Perimeter is
39.764 feet
The B dimension is
3.514 feet
The
C dimension is 2.485 feet
The
D dimension is 12.989 feet
The
diameter of the inscribed circle is 12 feet.
The
diameter of the circumscribed circle is 12.989
feet.
Note,
In this example my chosen starting point is the
Width.
However since the
Width, the Side, the Area, the Perimeter, the
B, C, D, dimensions and
the inscribed and circumscribed circles are
all related, by using my formulas, any one or all of these parameters can just as
easily be found by starting from any one of them.
|
For
many years I've
wrestled with my questions regarding the regular octagon
as to what provable relationships could there be pertaining to
my observations and deductions as to the square root of 2
minus 1.
AND NOW AFTER ALL THESE
YEARS, Read
my brother, Noel Reekie's Octagon Proof.
2008.
Back to Square One. My
latest discovery and mystery.
1.0824
is my multiplier of the Width to get the Diagonal.
2.6135
is my multiplier of the Side to get the Diagonal.
Divide
the 1st by the 2nd and the answer is
0.4142
again,
that esoteric
square root
of 2, minus 1
2012.
Divide the 2nd by the 1st and the answer is the sq. rt. of 2
plus 1.
Multiply the 2nd by the 1st and the answer is 2 times the
sq. rt. of 2.
Pertaining
to Octagon Formulas: without exception; every equation, that
I come up with, includes the Square Root of 2.
Fascinating
fascination.